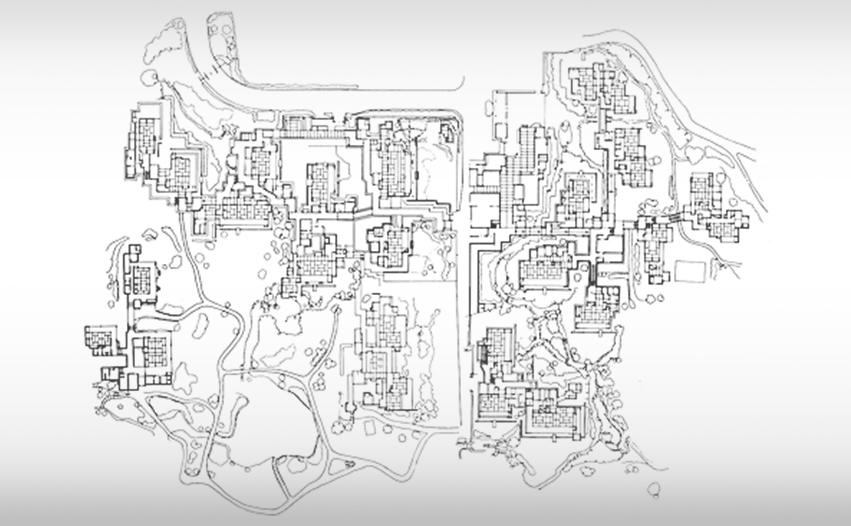
頂点とは、座標情報を持っている三次元空間上の任意の一点を指します。この点を3つ結んだ面が、三角形ポリゴンです。頂点を結ぶ順番で裏表が存在し、CADやWEB GL等ではカリングを行うことができます。
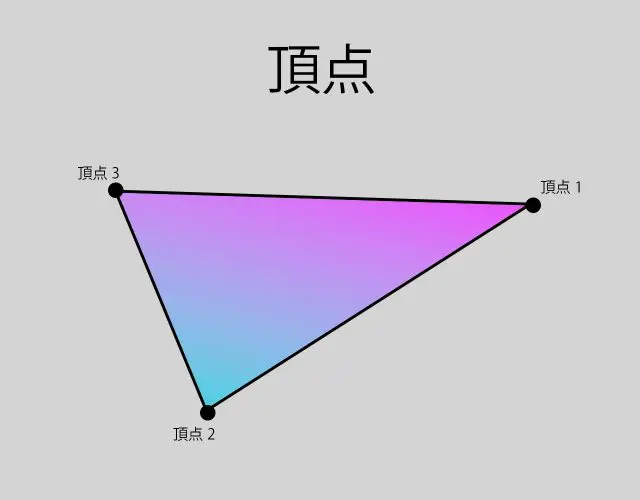
頂点
ここでは、頂点について解説していきます。
頂点
- 頂点座標
- 頂点インデックス
- 法線
頂点座標
3Dで最も簡単にレンダリングすることができるのはポリゴンです。ポリゴンを描画する際、頂点と呼ばれる3D空間上の点を座標で定義します。通常3Dソフト全般は、三角形ポリゴンなのですが、3Dビュー上では四角形になっていることが多々あります。
※システム上では三角形表示
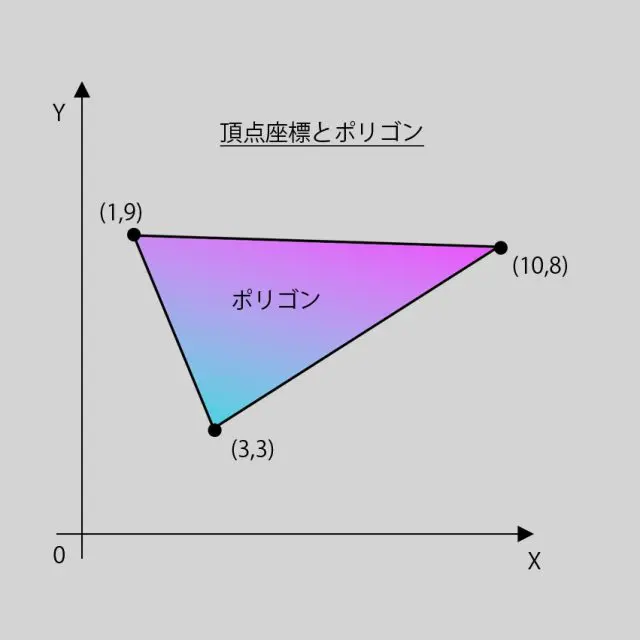
頂点座標とポリゴン
データとしては、頂点座標を持っており、描画時に頂点座標からポリゴンの形が計算されます。
頂点インデックス
頂点インデックスとは、頂点に割り当てられた番号のことを言います。ポリゴンを作るためにどの頂点を使うかを頂点インデックスで指定します。
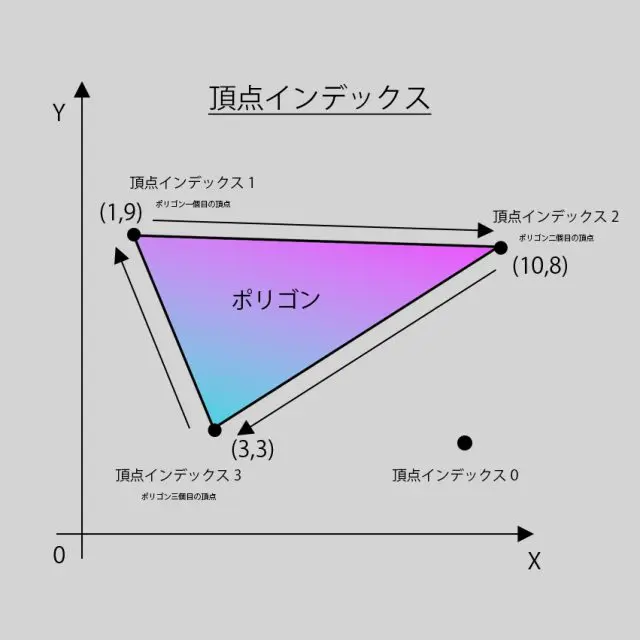
頂点インデックス
頂点インデックスにより、三角ポリゴンを作成する際、頂点が3つ以上あっても三角ポリゴンを作成することができます。他に頂点を指定する順番にも意味があります。ポリゴンには裏と表が存在し、頂点の選択順序で変わってきます。時計回りで選択した場合は表、反時計回りで選択したならば裏になります。(ゲームエンジンなどの場合)
※MAYAにも頂点の順序を転送というのが存在しますので良ければ調べてみてください。
法線
法線は、ポリゴンの頂点や面が向いてる方向を表すものです。長さが一の単位ベクトルで表され、フェース法線と頂点法線が存在します。
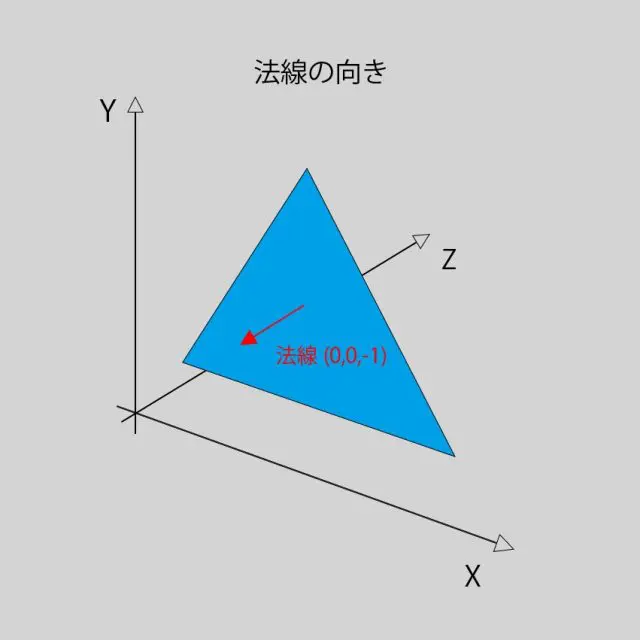
法線の向き
フェース法線
フェースの中央に表示される法線のことを指します。この法線はフェースに必ず直行する角度になっており、フェースの裏表を表します。
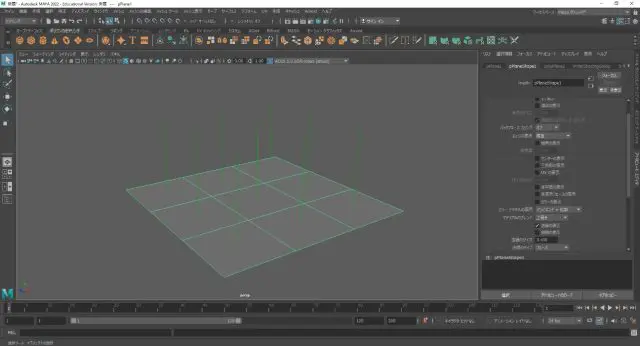
フェース法線
頂点法線
頂点上に表示される法線のことを指します。実際、頂点法線は頂点フェース単位で存在しているため、角度の編集が可能です。編集することによってフェースの形状を変えることなく陰影の調整を行うことができます。
※トゥーン表現などにて調整を行うことが多いです。
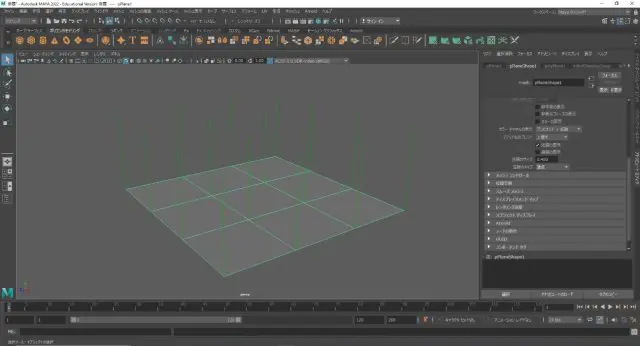
頂点法線
頂点フェース
MAYAの機能で両者を表示したものです。法線編集の際に非常に見やすく役立ちます。
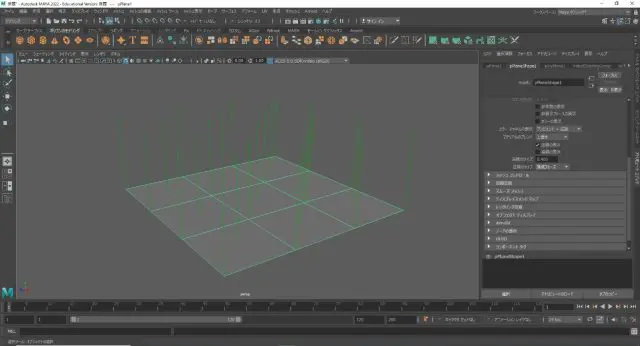
頂点フェース
今回は、MAYAにて説明しましたが、どの3Dソフトウェアにも関係しているので是非学んでみてください。

![お電話・FAXでのお問い合わせ [営業時間]10:00~17:00 土・日・祝日定休 TEL:045-321-1297 FAX:050-6860-5155 問い合わせ先](/wp-content/themes/cocoon-child-master/images/text_tel.gif)